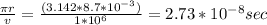Complete Question
The complete question is shown on the first uploaded image
Answer:
The time t required is

Step-by-step explanation:
When this proton move into the magnetic field region the magnetic field would cause it to move in a clockwise direction
The force which it would feel inside the field is mathematically denoted as follows
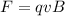
And this is the same thing as the force which keeps it around the circle without spiraling off and this is also know as centripetal force and it is mathematically
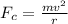
Since the two force are equal we can equate the formulas
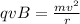
making r the subject of the formula
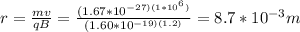
Now mathematically the total distance traveled is
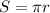
Since
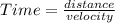
=