Question

An undiscovered planet, many lightyears from Earth, has one moon in a periodic orbit. This moon takes 1760 1760 × 103 seconds (about 2.0 × 10 1 2.0×101 days) on average to complete one nearly circular revolution around the unnamed planet. If the distance from the center of the moon to the surface of the planet is 285.0 285.0 × 106 m and the planet has a radius of 3.50 3.50 × 106 m, calculate the moon's radial acceleration a c ac .

Answer 1

`a_c=6.471(m)/(s^(2))`

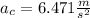
Step-by-step explanation:

We can calculate the magnitude of the tangential velocity of the moon, using the equation:

`v=(2\pi R)/(\tau)`

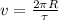
(This works, since velocity is defined as distance over time; in this case the distance is 2πR and the time is the period τ)

Next, from the equation of the centripetal acceleration we have:

`a_c=(v^(2) )/(R)\\\\a_c=(4\pi^(2)R)/(\tau^(2) )`

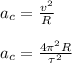
Be careful, the radius of the orbit R is equal to the distance from the center of the moon to the center of the planet. So we have to sum the distance from the center of the moon to the surface of the planet and the radius of the planet to obtain R:

`R=285.0*10^(6) m+3.50*10^(6) m=288.5*10^(6)m`

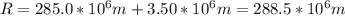
Finally, plugging the given values into the centripetal acceleration formula, we have:

`a_c=(4(3.141)^(2)(288.5*10^(6)m))/((1760*10^(3)s)^(2)) =6.471(m)/(s^(2))`

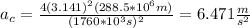
In words, the moon's radial acceleration a_c is 6.471m/s².