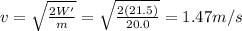Question

A luggage handler pulls a 20.0 kg suitcase up a ramp inclined at 34.0 ∘ above the horizontal by a force F⃗ of magnitude 163 N that acts parallel to the ramp. The coefficient of kinetic friction between the ramp and the incline is μk = 0.300. The suitcase travels 3.90 m along the ramp.A) the work done on the suitcase by force F.B) the work done on the suitcase by the gravitational force.C) the work done on the suitcase by the normal force.D) the work done on the suitcase by the friction force.E) the total work done on the suitcase.F) if the velocity of the suitcase is zero at the bottom of the ramp,what is its velocity after it has travelled 4.60 m along the ramp.

Answer 1

A) 635.7 J

B) -427.4 J

C) 0 J

D) -190.1 J

E) +18.2 J

F) 1.47 m/s

Step-by-step explanation:

A)

The work done by a force on an object is given by

`W=F_p d`

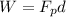
where

`F_p` is the component of the force in the direction of the displacement

d is the displacement of the object

In this problem:

F = 163 N is the magnitude of the force, which acts along the ramp; so, the force is parallel to the displacement,

`F_p = F = 163 N`

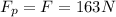
d = 3.90 m is the displacement of the suitcase

Therefore, the work done by force F on the suitcase is

`W_F=(163)(3.90)=635.7 J`

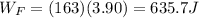
B)

In order to find the work done by the gravitational force, we use again the equation

`W=F_p d`

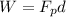
In this case, we need to us the component of the gravitational force parallel to the ramp; this is given by

`F_p = mg sin \theta`

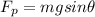
where

m = 20.0 kg is the mass of the suitcase

`g=9.8 m/s^2` is the acceleration due to gravity

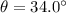`\theta=34.0^(\circ)` is the angle of the ramp

Moreover, this force acts down along the ramp, while the displacement is up along the ramp, so the work done will have a negative sign; so, the work done by the gravitational force is:

`W_g = -mg sin \theta d=-(20.0)(9.8)(sin 34^(\circ))(3.90)=-427.4 J`

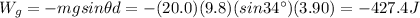
C)

In order to find the work done by the normal force, we use again the equation

`W=F_p d`

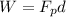
Where
`F_p` is the component of the normal force parallel to the ramp.

The normal force is the reaction force exerted by the surface of the ramp on the suitcase: it acts perpendicular to the ramp.

This means that the component of the normal force in the direction parallel to the ramp is zero:

`F_p = 0`

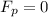
And therefore, the work done by the normal force on the suitcase is simply zero:

`W_N=0`

D)

Here the frictional force acts along the ramp, but in the direction opposite to the motion of the suitcase. Therefore, the work done by the frictional force will have a negative sign:

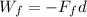`W_f=-F_f d` (1)

Where the frictional force can be written as

`F_f=\mu_k N`

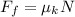
where

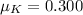`\mu_K=0.300` is the coefficient of kinetic friction

N is the normal force

The normal force is equal to the component of the weight perpendicular to the ramp, so:

`N=mg cos \theta`

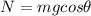
Substituting everything into (1), we find:

`W_f=-\mu_k mg cos \theta d`

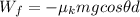
And therefore, the work done by friction is:

`W_f=-(0.300)(20.0)(9.8)(cos 34^(\circ))(3.90)=-190.1 J`

E)

The total work done on the suitcase is the algebraic sum of the works done by each force on the suitcase.

From part A-D, we have:

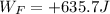`W_F=+635.7 J` is the work done by the force F

`W_g=-427.4 J` is the work done by the gravitational force

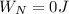`W_N=0 J` is the work done by the normal force

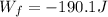`W_f=-190.1 J` is the work done by the friction force

Therefore, the total work done on the suitcase is:

`W=W_F+W_g+W_N+W_f=+635.7+(-427.4)+0+(-190.1)=+18.2 J`

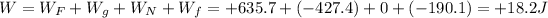
F)

The total work done by the forces on the suitcase along 3.90 m was

`W=+18.2 J`

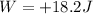
Since the work done by each force is proportional to the distance covered by the suitcase, the total work done along a distance of 4.60 m will be

`W'=(+18.2) \cdot (4.60)/(3.90)=+21.5 J`

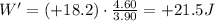
According to the work-energy theorem, the work done on the suitcase is equal to its change in kinetic energy; since the suitcase starts from rest, its initial kinetic energy is zero, so the work done is simply equal to the final kinetic energy:

`W'=(1)/(2)mv^2`

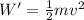
where

m = 20.0 kg is the mass

v is the final velocity of the suitcase

And solvign for v, we find

`v=\sqrt{(2W')/(m)}=\sqrt{(2(21.5))/(20.0)}=1.47 m/s`