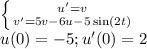Question

Consider the initial value problem:

y" - 5y' + 6y = -5sin(2t); y(0) = -5, y'(0) = 2
Write the differential equation above as a first-order system for the unknowns u, v, where u=y and v is defined as in the lecture notes. You do not need to solve the system.

Answer 1

`\left \{ {{u'=v} \atop {v'=5v-6u-5\sin(2t)}} \right. \\u(0)=-5;u'(0)=2`

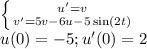
Explanation:

The given initial value problem is;

`y''-5y'+6y=-5\sin(2t)---(1)\\y(0)=-5,y'(0)=2`

Let

`u(t)=y(t)----(2)\\v(t)=y'(t)----(3)`

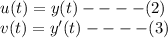
Differentiating both sides of equation (1) with respect to
`t`, we obtain:

`u'(t)=y'(t)---(4)\\ \\\implies u'(t)=v(t)---(5)`

Differentiating both sides of equation (2) with respect to
`t` gives:

`v'(t)=y''(t)----(6)`

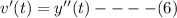
From equation (1),

`y''=5y'-6y-5\sin(2t)\\y''=5v(t)-6u(t)-5\sin(2t)\\\implies v'(t)=5v(t)-6u(t)-5\sin(2t)----(7)`

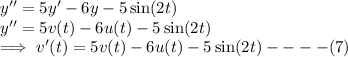
Putting t=0 into equation (2) yields

`u(0)=y(0)\\\implies u(0)=-5`

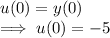
Also putting t=0 into equation (3)

`u'(0)=y'(0)\\u'(0)=2`

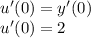
The system of first order equations is:

`\left \{ {{u'=v} \atop {v'=5v-6u-5\sin(2t)}} \right. \\u(0)=-5;u'(0)=2`