Question

Left on together, the cold and hot water faucets of a certain bathtub take 5 minutes to fill the tub. If it takes the hot water faucet 15 minutes to fill the tub by itself, how long will it take the cold water faucet to fill the tub on its own? Do not do any rounding.

Answer 1

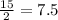`(15)/(2)=7.5` minutes.

Explanation:

Let t represent time taken by cold water faucet in minutes to fill the tub.

Part of tub filled by cold water faucet in one minute would be
`(1)/(t)`.

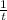We have been given that it takes the hot water faucet 15 minutes to fill the tub by itself, so art of tub filled by hot water faucet in one minute would be
`(1)/(15)`.

We are also told that left on together, the cold and hot water faucets of a certain bathtub take 5 minutes to fill the tub, so part of tub filled by both faucets in one minute would be
`(1)/(5)`.

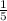We can represent part of tank filled by both faucets in one minute as:

`(1)/(15)+(1)/(t)=(1)/(5)`

`(1)/(15)\cdot 15t+(1)/(t)\cdot 15t=(1)/(5)\cdot 15t`

`t+15=3t`

`t-t+15=3t-t`

`15=2t`

`2t=15`

`(2t)/(2)=(15)/(2)`

`t=7.5`

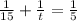
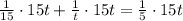
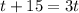
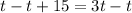
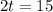
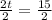
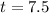
Therefore, it will take 7.5 minutes for the cold water faucet to fill the tub alone.