Question

A 7.13 kg bowling ball moves at 4.14 m/s. How fast must a 2.34 g Ping-Pong ball move so that the two balls have the same kinetic energy? Answer in units of m/s.

Answer 1

243.43 m/s

Step-by-step explanation:

Hello,I can help you with this.

the kinetic energy is asociated to the mass and the speed of an object,and it is given by:

`E_(k)=(1)/(2)mv^(2)`

where:

`E_(k)` is the kinetic energy

m is the mass of the object

v is the speed of the object

Step 1

let

bowling ball =mass1=7.13 kg

Speed(1)=4.14 m/s

Ping-Pong ball

mass2=2.34 g

it is given in grams so we have to convert into Kg (dividing by 1000,1kg=1000 g)

`2.34g((1kg)/(1000g) )=0.00234kg`

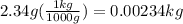
so, mass2=0.00234kg

Step 2

according to the problem both have equal Kinetic energy

`E_(1)=(1)/(2)m_(1) v_(1) ^(2)\\E_(2)=(1)/(2)m_(2) v_(2) ^(2)\\(1)/(2)m_(1) v_(1) ^(2)=(1)/(2)m_(2) v_(2) ^(2)\\isolate\ v_(2) \\m_(1) v_(1) ^(2)=m_(2) v_(2) ^(2)\\(m_(1) v_(1) ^(2))/(m_(2))=v_(2) ^(2) \\v_(2)=\sqrt{(m_(1) v_(1) ^(2))/(m_(2))}\\v_(2)=\sqrt{(7.13kg*(4.41(m)/(s)) ^(2))/(0.00234kg)} \\\\v_(2)=\sqrt{59258.526(m^(2) )/(s^(2) ) } \\\\\\v_(2)=243.43 m/s`

so the speed of the ping-pong ball should be 243.43 m/s

Have a good day.