Answer:
b. Using the balances of 50 homeowners rather than 35, because using more data gives a smaller margin of error
Explanation:
We have that to find our
 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
95% confidence interval
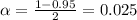
Now, we have to find z in the Ztable as such z has a pvalue of
 .
.
So it is z with a pvalue of
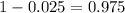 , so
, so

99% confidence interval

Now, we have to find z in the Ztable as such z has a pvalue of
 .
.
So it is z with a pvalue of
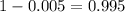 , so
, so

Now, find we find the width of our confidence interval M as such
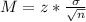
So, as n increases, the width of the confidence interval decreases.
From the examples above, we can also conclude that as the confidence level increases, so does the value of z, which means that the width of the interval increases.
Which of the following would correctly produce a confidence interval with a smaller margin of error than this 95% confidence interval?
For a smaller margin of error, we need to have a bigger sample size.
So the correct answer is:
b. Using the balances of 50 homeowners rather than 35, because using more data gives a smaller margin of error