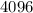Explanation:
We have , to simplify a complex expression . Basically a complex expression in the form a + ib , where i =
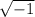 and is called iota.
and is called iota.
Expression:

⇒

⇒
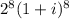
We know that the mod or modulus of a complex number in the form of
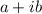 is represented by Z and Z =
is represented by Z and Z =
 . Computing mod of
. Computing mod of
 as :
as :
⇒
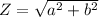
⇒
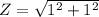
⇒
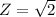
Putting value of
 as
as
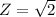 , we get:
, we get:
⇒
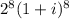
⇒
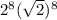
⇒
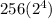
⇒