Question

A thin flake of mica ( n = 1.58 ) is used to cover one slit ofa double slit interference arrangement. The central point on theviewing screen is now occupied by what had been the seventh brightside fringe ( m = 7 ). If λ = 550 nm, what is thethickness of the mica?

Answer 1

the thickness of the mica is 6.64μm

Step-by-step explanation:

By definition we know that the phase between two light waves that are traveling on different materials (in this case also two) is given by the equation

`\Phi = 2\pi((L)/(\lambda)(n_1-n_2))`

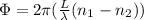
Where

L = Thickness

n = Index of refraction of each material

`\lambda = Wavelength`

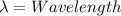
Our values are given as

`\Phi = 7(2\pi)L=tn_1 = 1.58n_2 = 1\lambda = 550nm`

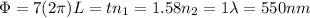
Replacing our values at the previous equation we have

`\Phi = 2\pi((L)/(\lambda)(n_1-n_2))7(2\pi) = 2\pi((t)/(\lambda)(1.58-1))`

`t = (7*550)/(1.58-1)\\t = 6637.931nm \approx 6.64\mu m`

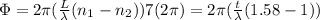
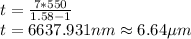
the thickness of the mica is 6.64μm