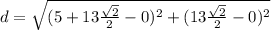Question

7. Andrew has map of a hidden treasure. He travels 5

meters 90°north, then he moves 13 meters 45° east
where treasure is hidden. Find the distance between
Andrew's initial location to the hidden treasure.

Answer 1

`d=16.9\ m`

Explanation:

Let

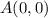`A(0,0)` -----> Andrew's initial location

we know that

1) He travels 5 meters 90°north

At this moment Andrew's location is

`B(0,0+5)\\B(0,5)`

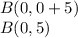
2) He moves 13 meters 45° east

At this moment Andrew's location is

`C(0+13cos(45^o),5+13sin(45^o))`

`C(0+13(√(2))/(2),5+13(√(2))/(2))`

`C(13(√(2))/(2),5+13(√(2))/(2))`

3) Find the distance between Andrew's initial location to the hidden treasure.

Find the distance between point A and point C

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

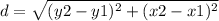
we have

`A(0,0)`

`C(13(√(2))/(2),5+13(√(2))/(2))`

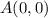
substitute the values

`d=\sqrt{(5+13(√(2))/(2)-0)^(2)+(13(√(2))/(2)-0)^(2)}`

`d=16.9\ m`