Answer:
(C) 5
Explanation:
Let x represent number of hours.
We have been given that running on a 10-mile loop in the same direction, Sue ran at a constant rate of 8 miles per hour.
Distance covered by Sue in x hours would be
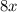 miles.
miles.
We are also told that Rob ran at a constant rate of 6 miles per hour, so distance covered by Rob in x hours would be
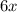 miles.
miles.
Since Sue needs to complete one more loop than Rob, so difference of distances covered by Sue and Rob's in x hours should be equal to 10 miles.
We can represent this information in an equation as:




Therefore, 5 hours later Sue will complete exactly 1 more lap than Rob and option C is the correct choice.