Answer:
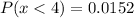
Explanation:
We are given a binomial distribution.
P(Success) = p = 0.6
We can calculate probability as:
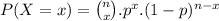
where n is the total number of observations, x is the number of success, p is the probability of success.
Now, we are given n = 12
We have to evaluate:
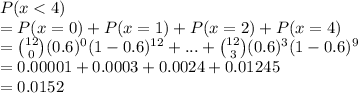
0.0152 is the required probability.