Answer:
So, the probability is P=0.2063.
Explanation:
We know that a university found that 20% of its students withdraw without completing the introductory statistics course.
We conclude that p=0.2 and q=1-0.2=0.8.
Assume that 20 students registered for the course.
So, n=20.
We calculate the probability that 2 or fewer will withdraw.
We know that

We use the formula

we get:

Therefore, we get
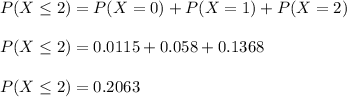
So, the probability is P=0.2063.