Question

Suppose a wheel with a tire mounted on it is rotating at the constant rate of 2.23 2.23 times a second. A tack is stuck in the tire at a distance of 0.379 m 0.379 m from the rotation axis. Noting that for every rotation the tack travels one circumference, find the tack's tangential speed

Answer 1

Step-by-step explanation:

The given data is as follows.

Angular velocity (
`\omega`) = 2.23 rps

Distance from the center (R) = 0.379 m

First, we will convert revolutions per second into radian per second as follows.

= 2.23 revolutions per second

=
`2.23 * 2 * 3.14 rad/s`

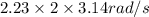
= 14.01 rad/s

Now, tangential speed will be calculated as follows.

Tangential speed, v =
`R * \omega`

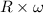
= 0.379 x 14.01

= 5.31 m/s

Thus, we can conclude that the tack's tangential speed is 5.31 m/s.