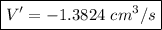Question

a spherical snowball is melting in such a way that it always retains spherical shape. The surface area of the snowball is decreasing at the rate of 2 cubic centimeters per second. Find the rate of change of the volume when the surface area is 24 cm^2

Answer 1

`V'=-1.3824\ cm^3/s`

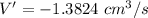
Explanation:

Rate of Change

The surface area of a sphere of ratio r is

`\displaystyle A=4\pi r^2`

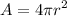
And its volume is

`\displaystyle V=(4)/(3)\pi r^3`

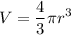
We know the surface area is
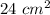`24\ cm^2`, let's find the ratio

`\displaystyle r=\sqrt{(A)/(4\pi )}=\sqrt{(24)/(4\pi )}=1.382\ cm`

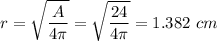
We'll find the rate of change of the surface area with respect to the time by taking the derivative

`\displaystyle A'=8\pi r r'`

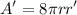
Solving for r'

`\displaystyle r'=(A')/(8\pi r )`

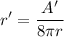
Since

`A'=-2 \ cm^2/s`

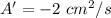
(note the correction of the units)

`\displaystyle r'=(-2)/(8\pi r )=-0.0576\ cm/s`

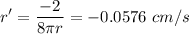
The change of the volume is obtained by taking the derivative:

`V'=4\pi r^2 r'=4\pi \cdot 1.382^2 \cdot (-0.0576)`

`\boxed{V'=-1.3824\ cm^3/s}`