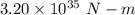Answer:
(a). The rotational inertia is
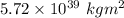
(b). The magnitude of the magnetic torque is
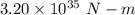
Step-by-step explanation:
Given that,
Mass of neutron
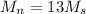
Density of neutron
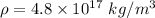
(a). We need to calculate the rotational inertia
Using formula of rotational inertia for sphere
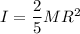 ...(I)
...(I)
We know that,
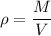
Put the value of volume
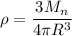

Put the value of R in equation (I)
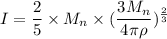
Put the value into the formula

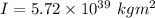
The rotational inertia is
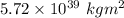 .
.
(b). We need to calculate the magnitude of the magnetic torque
Using formula of torque
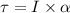
Put the value into the formula
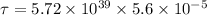
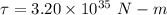
The magnitude of the magnetic torque is
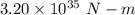
Hence, (a). The rotational inertia is
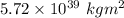
(b). The magnitude of the magnetic torque is