Question

Maya drove to the mountains last weekend. There was heavy traffic on the way there, and the trip took 12 hours. When Maya drove home, there was no traffic and the trip only took 8 hours. If her average rate was 20 miles per hour faster on the trip home, how far away does Maya live from the mountains?

Answer 1

480 miles.

Explanation:

Let x represent the distance between Maria's house and mountains ans r represent Maria's rate for going trip.

We have been given that there was heavy traffic on the way there, and the trip took 12 hours.

`\text{Distance}=\text{Rate}* \text{Time}`

`x=12r`

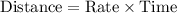
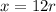
We are also told that hen Maya drove home, there was no traffic and the trip only took 8 hours. Maria's average rate was 20 miles per hour faster on the trip home.

So Maria's speed while returning back would be
`r+20`.

`x=8(r+20)`

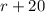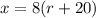
Upon equating both distances, we will get:

`12r=8(r+20)`

`12r=8r+160`

`12r-8r=8r-8r+160`

`4r=160`

`r=(160)/(4)`

`r=40`

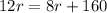
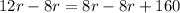
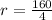
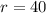
Upon substituting
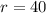`r=40` in equation
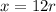`x=12r`, we will get:

`x=12r\\\\x=12(40)\\\\x=480`

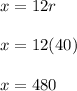
Therefore, Maya live 480 miles away from the mountains.