Question

How do you solve 4x^2 - 8x + 4 = 0 as completing the square? Is there a solution?

Answer 1

1

Explanation:

Yes, there is a solution! You first look for a common factor to factor away. Observing, you see that there is common multiple of 4, so your equation becomes
`4(x^2-2x+1)=0`. Dividing away the 4, we get
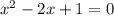`x^2-2x+1=0`. From here, we can complete the square:
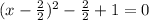`(x-(2)/(2))^2-(2)/(2)+1=0` which is equal to
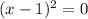`(x-1)^2=0`. When x=1, both sides of the equation equal 0, so x=1.