Question

A bowling ball weighing 71.2 N is attached to the ceiling by a 3.30 m rope. The ball is pulled to one side and released; it then swings back and forth like a pendulum. As the rope swings through its lowest point, the speed of the bowling ball is measured at 5.60 m/s. At this instant, what are

a. The acceleration of the bowling ball, in magnitude and direction.
b. The tension in the rope?

Answer 1

a. The acceleration of the bowling ball is 9.5 m/s² toward the center

b. The tension in the rope is 140.24 N

Step-by-step explanation:

given information:

ball weight, W = 71.2 N

the length of rope, R = 3.30 m

ball speed, v = 5.60 m/s

a. The acceleration of the bowling ball, α

α =
`(v^(2) )/(R)`

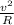
where

α = the acceleration

v = the speed

R = radius

thus

α =
`(v^(2) )/(R)`

=
`(5.60^(2) )/(3.3)`

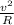
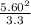
= 9.5 m/s² toward the center

b. The tension in the rope?

according to the Newton's second law

ΣF = m a

where

F = force

m = mass

a = acceleration

so,

ΣF = m a

T - W = m a

T = m a + W

= (W a/g) + W

= (71.2 x 9.5/9.8) + 71.2

= 140.24 N