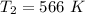Question

A gas occupies a volume of 444 mL at 273 K and 79.0 kPa. What is the final kelvin temperature when the volume of the gas is changed to 1880 mL and the pressure is changed to 38.7 kPa

Answer 1

Therefore,

The final kelvin temperature when the volume of the gas is changed is

`T_(2)=566\ K`

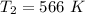
Step-by-step explanation:

Given:

`V_(1)=444\ ml\\T_(1)=273\ K\\P_(1)=79\ kPa`

`V_(2)=1880\ ml\\P_(2)=38.7\ kPa`

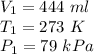
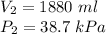
To Find:

`T_(2)=?`

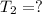
Solution:

Combined Gas Law:

The combined gas law combines the three gas laws:

Boyle's Law, Charles' Law, and Gay-Lussac's Law.

It states that the ratio of the product of pressure and volume and the absolute temperature of a gas is equal to a constant.

Hence,

`(P_(1)V_(1))/(T_(1))=(P_(2)V_(2))/(T_(2))`

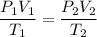
Substituting the values we get

`T_(2)=(P_(2)V_(2)T_(1))/(P_(1)V_(1))`

`T_(2)=(38.7* 1880* 273)/(79* 444)=566.26\approx 566\ K`

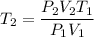
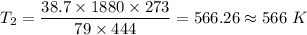
Therefore,

The final kelvin temperature when the volume of the gas is changed is

`T_(2)=566\ K`