Answer:
(a) Test statistics = 1.442
(b) P-value = 0.081
Explanation:
We are given that a cereal company claims the mean sodium content in one serving of its cereal is no more than 230 mg. For this a random sample of 52 servings has a mean sodium content of 232 mg and a standard deviation of 10 mg.
We have to test whether company's claim was true or not.
Let, Null Hypothesis,
 :
:

 230 mg {means that the company claims of mean sodium content in one serving of its cereal is no more than 230 mg is true}
230 mg {means that the company claims of mean sodium content in one serving of its cereal is no more than 230 mg is true}
Alternate Hypothesis,
 :
:
 > 230 mg {means that the company claims the mean sodium content in one serving of its cereal is no more than 230 mg is not true}
> 230 mg {means that the company claims the mean sodium content in one serving of its cereal is no more than 230 mg is not true}
(a) The test statistics that will be used here is One sample t-test statistics;
T.S. =
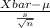 ~
~

where, Xbar = sample mean sodium content = 232 mg
s = sample standard deviation = 10 mg
n = sample of servings = 52
So, test statistics =
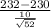 ~
~
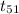
= 1.442
Therefore, the value of test statistics is 1.442 .
(b) Now, the P-value is given by = P(
 > test statistics)
> test statistics)
= P(
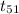 > 1.442) = 0.081 or 8.1%
> 1.442) = 0.081 or 8.1%
Since, P-value is greater than the significance level as 8.1% > 5%, so we have insufficient evidence to reject null hypothesis and conclude that company's claim was true.