Question

Let ˆθ be a statistic that is normally distributed with mean θ and standard error σθˆ. Show that 100(1 − α)% confidence interval for θ is given by: ˆθ ± z α 2 σθˆ

Answer 1

`\hat{\theta} \pm z_{(\alpha)/(2)}(\hat{\sigma_(\theta)})`

Explanation:

We are given the following in the question:

`\hat{\theta}` is distributed normally.

Mean =
`\hat{\theta}`

Standard error =
`\hat{\sigma_(\theta)}`

Significance level =
`\alpha`

Thus, the confidence percentage is

`100(1 - \alpha)\%`

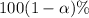
Confidence interval:

`\mu \pm z_(critical)(\sigma)/(√(n))`

`\mu \pm z_(critical)(\text{Standard error})`

`z_(critical)\text{ at}~\alpha = z_{(\alpha)/(2)}`

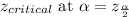
Putting the values, we get,

`\hat{\theta} \pm z_{(\alpha)/(2)}(\hat{\sigma_(\theta)})`

which is the required confidence interval.