Answer:
Part a: The value of Y_A and Y_B are
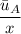 and
and
 respectively.
respectively.
Part b: Y_A and Y_B are given as
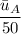 and
and
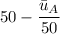 respectively for maximization of Y_B
respectively for maximization of Y_B
Part c: The condition for the Pareto efficient allocation is Y_A=Y_B
As the value of Y_A and Y_B are not equal in part 2 thus the condition is not Pareto efficient
Step-by-step explanation:
Part a
For the value of the utility function is given as
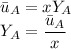
Also the YB is given as
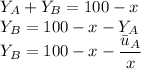
So the value of Y_A and Y_B are
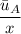 and
and
 respectively.
respectively.
Part b:
Now
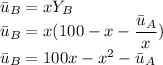
For the maximization
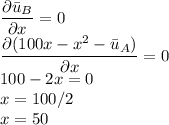
From question 1 Y_A and Y_B are given as
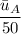 and
and
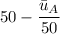 respectively for maximization of Y_B
respectively for maximization of Y_B
Part c:
At the Pareto efficient allocation
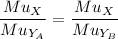
This is simplified to
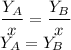
The condition for the Pareto efficient allocation is YA=YB
As the value of YA and YB are not equal in part 2 thus the condition is not Pareto efficient