Question

Suppose that the number of airplanes arriving at an airport per minute is a Poisson process. The mean number of airplanes arriving per minute is 3. The probability that exactly 6 planes arrive in the next minute is 0.05041.True / False.

Answer 1

The given statement is True.

Explanation:

We are given that the number of airplanes arriving at an airport per minute is a Poisson process with the mean number of airplanes arriving per minute is 3.

Let X = Distribution of number of airplanes arriving at an airport per minute

So, X ~ Poisson(
`\lambda`)

The mean of Poisson distribution is given by, E(X) =
`\lambda` = 3

which means, X ~ Poisson(3)

The probability distribution function of a Poisson random variable is:

`P(X=x)=(e^(-\lambda)\lambda^(x))/(x!); for x=0,1,2,3...`

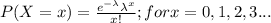
Probability that exactly 6 planes arrive in the next minute = P(X = 6)

P(X = 6) =
`(e^(-3)*3^(6))/(6!)` =
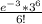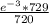`(e^(-3)*729)/(720)` = 0.05041

Therefore, the given statement is true.

Answer 2

`P(X=6)`

And using the probability mass function we got:

`P(X=6) =3^6 (e^(-3))/(6!)=0.05041`

So then we can conclude that the statement is True.

Explanation:

Definitions and concepts

The Poisson process is useful when we want to analyze the probability of ocurrence of an event in a time specified. The probability distribution for a random variable X following the Poisson distribution is given by:

`P(X=x) =\lambda^x (e^(-\lambda))/(x!)`

And the parameter
`\lambda= 3` represent the average ocurrence rate per unit of time.

Solution to the problem

For this case we want to find this probability:

`P(X=6)`

And using the probability mass function we got:

`P(X=6) =3^6 (e^(-3))/(6!)=0.05041`

So then we can conclude that the statement is True.