Question

Mike Polanski is 30 years of age and his salary next year will be $40,000. Mike forecasts that his salary will increase at a steady rate of 5% per annum until his retirement at age 60.

Required:

a. If the discount rate is 8%, what is the PV of these future salary payments?
b. If Mike saves 50/0 of his salary each year and invests these savings at an interest rate of 8%, how much will he have saved by age 60?
c. If Mike plans to spend these savings in even amounts over the subsequent 20 years, how much can he spend each year?

Answer 1

present value = $760662.5271

future value = $382714.30

spend each year = $38980.29

Step-by-step explanation:

given data

age = 30 year

salary next year = $40,000

salary increase steady rate = 5% per annum

solution

we will apply here here Growing Annuity formula that is express as

present value =
`C[(1)/(r-g)-(1)/(r-g)(((1+g)^T)/((1+r)^T))]` ....................1

here r is discount rate and g is increase per annum and C is salary and T is time period

so put here value in equation 1 we get

present value =
`\$40,000* [(1)/(0.08-0.05)-(1)/(0.08-0.05)(((1+0.05)^(30))/((1+0.08)^(30)))]`

present value = $760662.5271

and

here 5% of present value of salaries is

= 0.05 × $760662.5271

= $38033.1264

so here future value of money saving is

future value = present value ×
`(1+r)^T` ....................2

put here value

future value = $38033.1264 ×
`(1+0.08)^(30)`

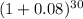
future value = $382714.30

and

now we get here savings spend each year C that is get by present value formula that is express as

present value =
`C[(1)/(r)-(1)/(r*(1+r)^t)]` ..............3

here r is interest Rate and t is time period i.e 20 yr

put her value and we get

$382714.30 = C
`[(1)/(0.08)-(1)/(0.08-(1+0.08)^2^0)]`

solve it we get

C = $38980.29