Question

Conduct an individual test on each of the variables. What is the decision rule at the 0.05 level of significance? (Negative amounts should be indicated by a minus sign. Round your answers to 3 decimal places.)

Answer 1

Explanation:

Hello!

Given the data of the multiple linear regression (see attachment) You have to conduct the individual tests for the five independent variables proposed to determine which one is significantly relevant for the regression.

The individual hypothesis tests of the multiple regression are the same as conducting the analysis for simple linear regression. The parameter of interest will be the population slope of the given variable, βi, and the statistic will be the Student's t:
`t= (b_i-\beta_i )/(Sb) ~ t_(n-2)`

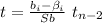
All hypothesis tests will be two tailed, so using α: 0.05, the critical region and decision rule for the five tests will be:

`t_(n-2;\alpha /2)= t_(23;0.025)= -2.069`

`t_(n-2;1-\alpha /2)= t_(23;0.975)= 2.069`

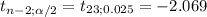
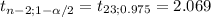
If
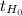`t_(H_0)` ≤ -2.069 or if
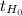`t_(H_0)` ≥ 2.069, then the decision is to reject the null hypothesis.

If -2.060<
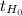`t_(H_0)` <2.069, then the decision is to not reject the null hypothesis.

Individual tests:

• For X₁

H₀: β₁=0

H₁: β₁≠0

α:0.05

b₁= 4.00

Sb₁= 1.50

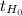`t_(H_0)`= 2.00

Since -2.060<
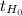`t_(H_0)` <2.069, the decision is to not reject the null hypothesis.

• For X₂

H₀: β₂=0

H₁: β₂≠0

α:0.05

b₂= 3.00

Sb₂= 0.20

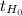`t_(H_0)`= 15.00

Since
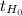`t_(H_0)` ≥ 2.069, the decision is to reject the null hypothesis.

• For X₃

H₀: β₃=0

H₁: β₃≠0

α:0.05

b₃= 0.20

Sb₃= 0.05

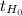`t_(H_0)`= 4.00

Since
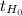`t_(H_0)` ≥ 2.069, the decision is to reject the null hypothesis.

• For X₄

H₀: β₄=0

H₁: β₄≠0

α:0.05

b₄= –2.50

Sb₄= 1.00

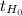`t_(H_0)`= –2.50

Since
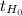`t_(H_0)` ≤ -2.069, the decision is to reject the null hypothesis.

• For X₅

H₀: β₅=0

H₁: β₅≠0

α:0.05

b₅= 3.00

Sb₅= 4.00

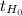`t_(H_0)`= 0.75

Since -2.060<
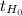`t_(H_0)` <2.069, the decision is to not reject the null hypothesis.

Even though it seems that the five independent variables altogether conform to a good regression model to explain/ predict the dependent variable. Individually there is not significant evidence to conclude that X₁ and X₅ are good predictors of Y. Therefore the model could work just as well using only X₂, X₃, X₄ as explanatory variables or there is a chance that without those two variables the regression will be even stronger.

I hope it helps!