Question

. An object has a position given by ~r(t) = [3.0 m − (4.00 m/s)t]ˆı + [6.0 m − (8.00 m/s2 )t 2 ]ˆ , where all quantities are in SI units. What is the magnitude of the acceleration of the object at time t = 5.00 s? (a) 8.94 m/s 2 (b) 0.00 m/s 2 (c) 16.0 m/s 2 (d) 8.00 m/s 2 (e) 4.00 m/s 2

Answer 1

(c) 16 m/s²

Step-by-step explanation:

The position is
`r(t) = [3.0 \text{ m} - (4.00 \text{ m/s})t]\hat{i} + [6.0 \text{m} - (8.00 \text{ m/s}^2 )t^2 ]\hat{j}`.

The velocity is the first time-derivative of r(t).

`v(t) = (d)/(dt)r(t) = -4.00\,\hat{i} -16t\,\hat{j}`

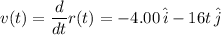
The acceleration is the first time-derivative of the velocity.

`a(t) = (d)/(dt) v(t) = -16\hat{j}`

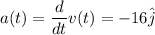
Since a(t) does not have the variable t, it is constant. Hence, at any time,

`a = -16\hat{j}`

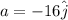
Its magnitude is 16 m/s².