Answer:
(a)
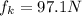
(b)
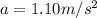
Step-by-step explanation:
First, we write the equations of motion of the crate for each axis:
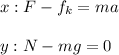
Since the kinetic frictional force is equal to
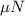 , and from the second equation we have that:
, and from the second equation we have that:
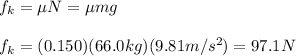
This means the frictional force has a magnitude of 97.1N (a).
Next, we use this value to calculate the magnitude of acceleration from the first equation of motion:
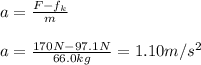
In words, the magnitude of the crate's acceleration is 1.10m/s² (b).