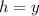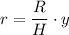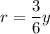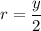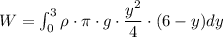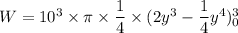Question

A tank in the shape of an inverted right circular cone has height 6 meters and radius 3 meters. It is filled with 2 meters of hot chocolate. Find the work required to empty the tank by pumping the hot chocolate over the top of the tank

Answer 1

Explanation:

Given

Radius of cone
`R=3\ m`

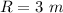
height of cone
`H=6\ m`

Chocolate is filled up to a height of
`h=2\ m`

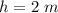
Work done to lift a body to a height h when F force is applied is given by

`W=Fh`

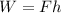
An infinitesimally slice of chocolate
`\Delta y` at a height of y has a radius

`r=(R)/(H)\cdot h`

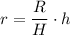
Volume of slice is
`dV=\pi r^2y`

`mass =\rho * dV`

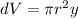
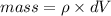
This mass need to be raised to a height of 6-y which requires a work of

`dW=\rho (\pi r^2ydy)g(6-y)`

To empty the tank

`W=\int_(0)^(3)\rho \cdot \pi \cdot g\cdot r^2\cdot (6-y)dy`

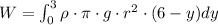
at
`h=y`

`r=(R)/(H)\cdot y`

`r=(3)/(6)y`

`r=(y)/(2)`

`W=\int_(0)^(3)\rho \cdot \pi \cdot g\cdot (y^2)/(4)\cdot (6-y)dy`

`W=10^3* \pi * (1)/(4)* (2y^3-(1)/(4)y^4)_0^3`

`W=259.80\ kJ`