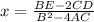Question

A critical point of f(x, y) is any point where both partial derivatives vanish. Find all critical points of (a) f(x, y) = x 2 − 3xy + y 2 + 2x + 5 (b) f(x, y) = x 2 − 2xy + y 2 (c) f(x, y) = Ax2 + Bxy + Cy2 + Dx + Ey + F

Answer 1

Explanation:

`(a) f(x, y) = x^ 2-3xy + y ^2 + 2x + 5`

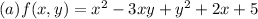
Let us find out partial derivatives

`f_x =2x-3y+2\\f_y = -3x+2y`

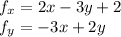
Equate these to 0 and solve

we get

`6x-9y+6 =0\\-6x+4y=0\\-5y+6 =0\\y=1.2 \\x=0.8`

Critical point (0.8,1.2)

b)
`f(x, y) = x^ 2 - 2xy + y^ 2\\f_x=2x-2y=0\\f_y = -2x+2y =0\\x=y`

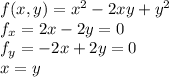
So (x=y) is the solution

c)
`f(x, y) = Ax^2 + Bxy + Cy^2 + Dx + Ey + F\\f_x=2Ax+By+D\\f_y=Bx+2cY+E`

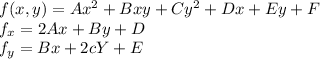
Equate to 0 and solve

2ABx + B^2y +DB =0

2ABx+4ACy +2AE =0

`y =(BD-2AE)/(B^2-4AC)`

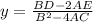
Similarly for x

4ACX + 2BCy +2CD =0

B^2 x +2BCy+BE=0

`x=(BE-2CD)/(B^2-4AC)`