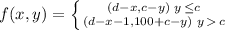Question

The price of an item you want to buy is given in dollars and cents. You pay for it in cash by giving the clerk d dollars and c cents. Write specifi cations for a function that computes the change, if any, that you should receive. Include a statement of purpose, the preconditions and postconditions, and a description of the arguments.

Answer 1

`f(x,y) = \left \{ {(d-x,c-y) \, \, {y \, \leq c} \atop (d-x-1, 100+c-y) \, \, {y \, > \, c}} \right.`

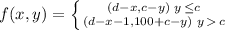
Where x is the amount of dollars the item costs and y is the amount of cents. The first entry of f(x,y) is the amount of dollars to be returned and the second entry is the amount of cents to be returned.

Explanation:

let f(x,y) be the function that computes the change.

The parameter x is the amount of dollars it costs and y is the amount of cents. both x and y should be integers and both of them should be positive or 0. Also y must be lower than 100, and x cant be bigger than d. Also if x = d, then it must happen that y ≤ c. The return value f(x,y) is a pair (a,b) where a and b satisfies the same conditions than the ordered pair (x,y) (the change cant be higher than the amount paid). a represents the amount of dollars that has to be returned and b the amount of cents.

Now, lets go to the formula. The formula should depend on wether y is higher than d or not, if that is the case, then after substracting x from d, we need to substract one more and add 100 cents to c-y (because we cant be given negative cents)

`f(x,y) = \left \{ {(d-x,c-y) \, \, {y \, \leq c} \atop (d-x-1, 100+c-y) \, \, {y \, > \, c}} \right.`