Answer:
Explanation:
Hello!
The objective is to determine if there is any difference between using iPads vs textbooks in teaching algebra.
Two middle school classes were selected, to eliminate any other source of variation, the same teacher taught both classes, and the materials were provided by the same author and publisher. After a month 10 students of each class were randomly selected and tested, their test scores were recorded:
X₁: test scores of students that used iPads to study.
n₁= 10
X[bar]₁= 86.8
S₁= 8.97
X₂: test scores of students that used regular textbooks to study.
n₂= 10
X[bar]₂= 79.5
S₂= 10.8
a.
H₀: μ₁=μ₂
H₁: μ₁≠μ₂
α:0.05
Assuming that both variables are normally distributed and the population variances are equal, the statistic to use is a Student t for two independent samples with pooled sample variance:
![t_(H_0)= \frac{(X[bar]_1-X[bar]_2)-(Mu_1-Mu_2)}{Sa*\sqrt{(1)/(n_1) +(1)/(n_2) } }](https://img.qammunity.org/2021/formulas/mathematics/college/sbi7g0vfvvlu1rxr9dly7dc8kb6faephmj.png)

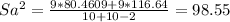
Sa= 9.93
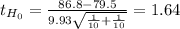
p-value: 0.118364
The p-value is greater than the significance level so the decision is to not reject the null hypothesis. This means that there is no significant evidence between the scores of the two groups.
b.
95% CI
(X[bar]-X[bar])±
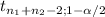 *
*
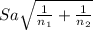

(86.8-79.5)±2.101*(9.93
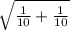 )
)
[-2.03; 16.63]
With a 95% confidence level, you'd expect that the interval [-2.03; 16.63] would contain the difference between the mean scores of the two classes.
c.
Considering that the null hypothesis wasn't rejected and that at the same level the confidence interval includes the zero, we can affirm that the format of the teaching materials, digital or regular textbooks, has no significant effect on the scores of the students.
I hope it helps!