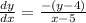Question

Find dy/dx, using implicit differentiation.

4x + 5y = xy
dy / dx = -(y-4) / (x-5)

1. Compare your answer with the result obtained by first solving for y as a function of x and then taking the derivative.
a. y =
b. dy dx =

2. Find dy/dx, using implicit differentiation.

Compare your answer with the result obtained by first solving for y as a function of x and then taking the derivative.
a. y =
b. dy / dx=

Answer 1

a)
`y=(4x)/(x-5)`

b)
`(dy)/(dx) =(-(y-4))/(x-5)`

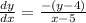
Explanation:

Step 1:-

Given 4x+5y = x y .......(1)

subtracting '5y' on both sides, we get

4x+5y-5y = x y - 5y

on simplification, we get

4x = y(x-5)

Dividing 'x-5' on both sides, we get

`y=(4x)/(x-5)`

Step 2:-

by using derivative formulas

`(dx^(n) )/(dx) = n x^(n-1)`

apply '
`(d)/(dx) (UV)= U(dV)/(dx) +V(dU)/(dx)`

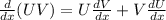
Differentiating equation (1) with respective to 'x' we get

`4+5(dy)/(dx) = x(dy)/(dx) +y(1)`

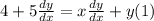
On simplification , taking common
`(dy)/(dx)`we get,

`5(dy)/(dx) -x(dy)/(dx) =y-4`

`(dy)/(dx) =(-(y-4))/(x-5)`