Question

A simple random sample of 60 items resulted in a sample mean of 80. The population standard deviation is σ = 15. a. Compute the 95% confidence interval for the population mean. b. Assume that the same sample mean was obtained from a sample of 120 times. Provide a 95% confidence interval for the population mean. c. What is the effect of a larger sample size on the interval estimate?

Answer 1

a) (76.21,83.79)

b) (77.32,82.68)

c) Interval decreases

Explanation:

We are given the following information in the question:

Sample size, n = 60

Sample mean = 80

Sample standard Deviation, s = 15

a) 95% Confidence interval:

`\mu \pm z_(critical)(\sigma)/(√(n))`

Putting the values, we get,

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

`80 \pm 1.96((15)/(√(60)) ) = 80 \pm 3.79 = (76.21,83.79)`

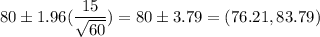
b) Sample size, n = 120

95% Confidence interval:

`80 \pm 1.96((15)/(√(120)) ) = 80 \pm 2.68 = (77.32,82.68)`

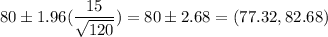
c) As observed increasing the sample size, the confidence interval become smaller.