Question

woman who weighs 500 N stands on an 8.0-m-long board that weighs 100 N. The board is supported at each end. The support force at the right end is 3 times the support force at the left end. How far from the right end is the woman standing

Answer 1

Step-by-step explanation:

Let us assume that W is the weight of the board and
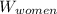`W_(women)` is the weight of women standing.

And, at the left end supporting force is F and at the right end supporting force is 3F.

So, when this system is in equilibrium then upward force will be equal to the downward force as follows.

`F + 3F = W + W_(women)`

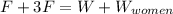
4F = 100 N + 500 N

F =
`(600)/(4)`

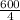
= 150 N

For system to be in static friction another condition is that net torque acting on the left end will be equal to zero.

Hence,
`\sum \tau` = 0

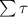`(3F * 8 m) - W (4 m) - W_(women) (8 m)` = 0

Putting the given values into the above formula as follows.

`(3F * 8 m) - W (4 m) - W_(women) (8 m)` = 0

`(3 * 150 N * 8 m) - 100 N (4 m) - 500 N (x)` = 0

x = 6.4 m

Therefore, at the left side distance from the women is 6.4 m.

And, distance from the right end will be as follows.

8 m - 6.4 m = 1.4 m