Answer:
99.5% confidence interval = [0.191 , 0.309]
Explanation:
We are given that in a sample of 432 people aged 65 and over, 108 of them had sleep apnea.
The pivotal quantity for 99.5% confidence interval for the proportion of those aged 65 and over who have sleep apnea is given by;
P.Q. =
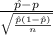 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion = 108/432 = 0.25
= sample proportion = 108/432 = 0.25
p = population proportion
n = sample size = 432
So, 99.5% confidence interval for the population proportion, p is given by;
P(-2.813 < N(0,1) < 2.813) = 0.995 {At 0.5% level of significance z table gives
critical value of 2.813}
P(-2.813 <
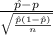 < 2.813) = 0.995
< 2.813) = 0.995
P(-2.813 *
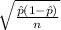 <
<
 < 2.813 *
< 2.813 *
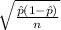 ) = 0.995
) = 0.995
P(
 - 2.813 *
- 2.813 *
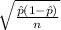 < p <
< p <
 + 2.813 *
+ 2.813 *
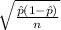 ) = 0.995
) = 0.995
99.5% confidence interval for p = [
 - 2.813 *
- 2.813 *
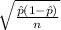 ,
,
 + 2.813 *
+ 2.813 *
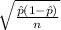 ]
]
= [0.25 - 2.813 *
 , 0.25 + 2.813 *
, 0.25 + 2.813 *
 ]
]
= [0.191 , 0.309]
Therefore, 99.5% confidence interval for the proportion of those aged 65 and over who have sleep apnea is [0.191 , 0.309] .