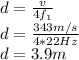Answer:
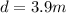
Step-by-step explanation:
The well is closed at bottom and opened at top.So we will have vibration corresponding to n=1,3,5,7......
Let the frequency of nth harmonic vibration is fn=110Hz.Then we have:

The nth harmonic is related to the fundamental frequency f₁ as fn=nf₁. Similarly fn+2=(n+2)f₁
Then we have
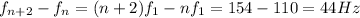
f₁ is common factor on left side.So we have
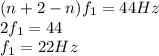
So the fundamental frequency of vibrations f₁=22Hz
Depth d of well is given by: