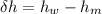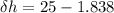Answer:
a)
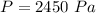
b)

Step-by-step explanation:
Given:
height of water in one arm of the u-tube,
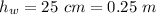
a)
Gauge pressure at the water-mercury interface,:
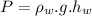
we've the density of the water
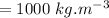

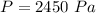
b)
Now the same pressure is balanced by the mercury column in the other arm of the tube:
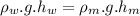
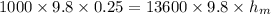
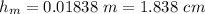
Now the difference in the column is :