Question

Two trains on separate tracks move toward each other. Train 1 has a speed of 145 km/h; train 2, a speed of 72.0 km/h. Train 2 blows its horn, emitting a frequency of 500 Hz. What is the frequency heard by the engineer on train 1

Answer 1

Therefore,

The frequency heard by the engineer on train 1

`f_(o)=603\ Hz`

Step-by-step explanation:

Given:

Two trains on separate tracks move toward each other

For Train 1 Velocity of the observer,

`v_(o)=145\ km/h=145* (1000)/(3600)=40.28\ m/s`

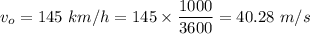
For Train 2 Velocity of the Source,

`v_(s)=90\ km/h=90* (1000)/(3600)=25\ m/s`

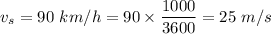
Frequency of Source,

`f_(s)=500\ Hz`

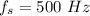
To Find:

Frequency of Observer,

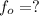`f_(o)=?` (frequency heard by the engineer on train 1)

Solution:

Here we can use the Doppler effect equation to calculate both the velocity of the source
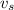`v_(s)` and observer
`v_(o)`, the original frequency of the sound waves
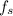`f_(s)` and the observed frequency of the sound waves
`f_(o)`,

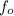The Equation is

`f_(o)=f_(s)((v+v_(o))/(v -v_(s)))`

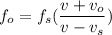
Where,

v = velocity of sound in air = 343 m/s

Substituting the values we get

`f_(o)=500((343+40.28)/(343 -25))=500* 1.205=602.64\approx 603\ Hz`

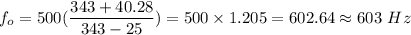
Therefore,

The frequency heard by the engineer on train 1

`f_(o)=603\ Hz`