Question

From a population that is not normally distributed and whose standard deviation is not known, a sample of 50 items is selected to develop an interval estimate for mean. Which of the following statements are true?

a) the standard normal distribution can be used
b) the t distribution with 50 degrees of freedom must be used
c) the t distribution with 49 degrees of freedom must be used
d) the sample size must be increased in order to develop an interval estimate

Answer 1

The correct approach for developing an interval estimate for the mean from a non-normally distributed population with unknown standard deviation and a sample size of 50 is to use the t distribution with 49 degrees of freedom.

Step-by-step explanation:

From a population that is not normally distributed and whose standard deviation is not known, a sample of 50 items is selected to develop an interval estimate for the mean. The correct statement in this scenario is that the t distribution with 49 degrees of freedom must be used, which corresponds to option c). This is because the sample standard deviation (s) is used as an estimate for the unknown population standard deviation (σ), and the degrees of freedom are equal to the sample size minus one (df = n - 1). As the sample size is greater than 30, the t distribution can still be used even if the population is not normally distributed.

It is not correct that the standard normal distribution can be used (option a), as it is more appropriate when the population standard deviation is known. Increasing the sample size (option d) is not necessary to develop an interval estimate since a sample of 50 is sufficient for the t distribution to be a reasonable approximation.

Answer 2

Correct option: c) the t distribution with 49 degrees of freedom must be used

Step-by-step explanation:

The (1 - α)% confidence interval for population mean (μ) is:

`CI=\bar x\pm z_(\alpha/2)(\sigma)/(√(n))`

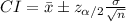
OR

`CI=\bar x\pm t_(\alpha/2, (n-1))(s)/(√(n))`

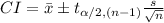
A t-interval is used when the there is no information provided about the population standard deviation and when the population is normally distributed.

In this case there is no information about the population standard deviation and the population is also not normally distributed.

But as the t-distribution is derived from the normal distribution, to construct a t-interval the sample drawn must be large, i.e. n > 30.

Because for large sample sizes the sampling distribution of sample means will follow a Normal distribution with mean μ of the population and standard deviation
`(s)/(√(n))`.

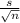In this case the sample size is, n = 50 > 30.

So a t distribution with n - 1 = 50 - 1 = 49 degrees of freedom will be used to construct the confidence interval for mean.