Question

The random variable X is exponentially distributed, where X represents the waiting time to be seated at a restaurant during the evening. If X has an average value of 19 minutes, what is the probability that the wait time is greater than 14 minutes

Answer 1

The probability that the wait time is greater than 14 minutes is 0.4786.

Explanation:

The random variable X is defined as the waiting time to be seated at a restaurant during the evening.

The average waiting time is, β = 19 minutes.

The random variable X follows an Exponential distribution with parameter
`\lambda=(1)/(\beta)=(1)/(19)`.

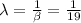The probability distribution function of X is:

`f(x)=\lambda e^(-\lambda x);\ x=0,1,2,3...`

Compute the value of the event (X > 14) as follows:

`P(X>14)=\int\limits^(\infty)_(14) {\lambda e^(-\lambda x)} \, dx=\lambda \int\limits^(\infty)_(14) {e^(-\lambda x)} \, dx\\=\lambda |(e^(-\lambda x))/(-\lambda)|^(\infty)_(14)=e^{-(1)/(19) *14}-0\\=0.4786`

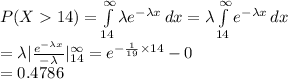
Thus, the probability that the wait time is greater than 14 minutes is 0.4786.