Question

A voltage source of 10.0 V is connected to a series RC circuit where R = 2.80 × 10 6 Ω, and C = 3.50 µF. Find the amount of time required for the current in the circuit to decay to 4.00% of its original value. Hint: This is the same amount of time for the capacitor to reach 96.0% of its maximum charge.

Answer 1

The amount of time is 31.45 sec.

Step-by-step explanation:

Given that,

Voltage = 10.0 V

Resistance
`R=2.80*10^(6)\ \Omega`

Capacitance
`C=3.50\ \mu F`

We need to calculate the time constant

Using formula of time constant

`\tau=RC`

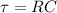
Put the value into the formula

`\tau=2.80*10^(6)*3.50*10^(-6)`

`\tau=9.8\ sec`

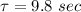
The amount of time required for the current in the circuit to decay to 4.00% of its original value.

We need to calculate the amount of time

Using formula of charge

`Q=Q_(max)(1-e^{(-t)/(RC)})`

Put the value into the formula

`96\%Q_(max)=Q_(max)(1-e^{(-t)/(RC)})`

`0.96=(1-e^{(-t)/(\tau)})`

`0.96=(1-e^{(-t)/(\tau)})`

`0.04=e^{(t)/(\tau)}`

`(-t)/(\tau)=ln(0.04)`

`t=3.21*9.8`

`t=31.45\ sec`

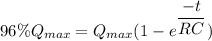
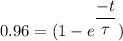
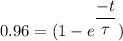
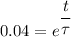
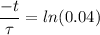
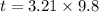
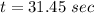
Hence, The amount of time is 31.45 sec.