Question

A plane flying horizontally at an altitude of 1 mi and a speed of 490 mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it is 2 mi away from the station. (Round your answer to the nearest whole number.) mi/h

Answer 1

The rate at which the distance from the plane to the station is increasing when it is 2 mi away from the station is 424 mi/h

Step-by-step explanation:

Given;

vertical position of the plane, h = 1 mi

when plane is 2 mi away from the station, this position and vertical position forms a right - angled triangle.

Let the vertical position = y = 1 mi

Let the 2 mi position = hypotenuse = p

Let the remaining side of the triangle, which is horizontal = x

x² = p² - y²

`x = √(p^2 -y^2) = √(2^2 -1^2) = √(3)`

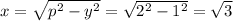
Again;

p² = x² + y²

the rate at which the distance from the plane to the station is increasing when it is 2 mi away from the station, can be determined by differentiating P with respect to time t.

`p^2.(dp)/(dt) = x^2.(dx)/(dt) +y^2.(dy)/(dt) \\\\2p.(dp)/(dt) = 2x.(dx)/(dt) + 2y.(dy)/(dt)\\\\2p.(dp)/(dt) = 2x.(dx)/(dt) + 0\\\\(dp)/(dt) = (2x)/(2p) .(dx)/(dt) \\\\(dp)/(dt) = (x)/(p) .(dx)/(dt) = (√(3))/(2) . 490((mi)/(h)) = 424 \ mi/h`

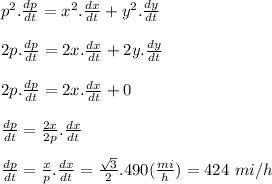
Therefore, the rate at which the distance from the plane to the station is increasing when it is 2 mi away from the station is 424 mi/h

Answer 2

Answer: 438.3 mph

Step-by-step explanation:

Let z be the distance from the plane to the station. You should draw a right triangle

for the diagram with z on the hypotenuse, 1 on the vertical side, and x on the horizontal

side. The 1 never changes, but x changes with time.

Find the attached file for the solution.