Question

Calculate ΔH∘f for NO(g) at 435 K, assuming that the heat capacities of reactants and products are constant over the temperature interval at their values at 298.15 K. Molar heat capacities of NO(g), N2(g), and O2(g) at 298.15 K are 29.86, 29.13, and 29.38 J⋅K−1⋅mol−1. The standard enthalpy of formation of NO(g) is 91.3 kJ⋅mol−1 at 298.15 K.

Answer 1

91383 J

Step-by-step explanation:

The equation of the reaction can be represented as:

`(1)/(2) N_(2(g))+(1)/(2) O_(2(g))` ------>
`NO_((g))`

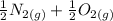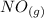
Given that:

The standard enthalpy of formation of NO(g) is 91.3 kJ⋅mol−1 at 298.15 K.

The equation below shown the reaction between the enthalpy of reaction at a particular temperature to another.

`\delta H^0__(R,T_2)` =
`\delta H^0__(R,T_1) } + \int\limits^(T_2)_(T_1) {\delta C_p(T')} \, dT'`

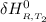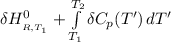
where:

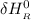`\delta H^0__(R)` = enthalpy of reaction

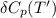`{\delta C_p(T')}` = the difference in the heat capacities of the products and the reactants.

∴

`\delta H^0__(R,435K)` =
`\delta H^0__(R,298.15K)`
`+`
`\int\limits^(435)_(298.15) {\delta C_p(T')} \, dT'`

=
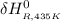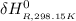
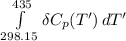
`1(91300 J.mol^(-1) ) +\int\limits^(435)_(298.15) [{(29.86)-(1)/(2)(29.38)-(1)/(2)29.13}]J.K^(-1).mol^(-1) \, dT'`

= 91300 J + (0.605 J.K⁻¹)(435-298.15)K

= 91382.79 J

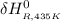`\delta H^0__(R,435K)` ≅ 91383 J