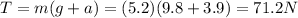Question

A bucket of water is being raised from a well using a rope. If the bucket of water has a mass of 5.2 kg, how much force (in N) must the rope exert on the bucket to accelerate it upward at 3.9 m/s2

Answer 1

71.2 N

Step-by-step explanation:

When the bucket of water is raised, there are two forces acting on it:

- The tension in the rope, T, upward

- The weight of the bucket,
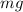`mg`, downward

According to Newton's second law of motion, the net force acting on the bucket must be equal to the product of the mass of the bucket and its acceleration, so we can write:

`T-mg=ma`

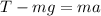
where:

T is the tension in the rope

m = 5.2 kg is the mass of the bucket of water

`g=9.8 m/s^2` is the acceleration due to gravity

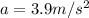`a=3.9 m/s^2` is the acceleration of the bucket (upward)

Solving the equation for T, we can find the tension that must be exerted in the rope:

`T=m(g+a)=(5.2)(9.8+3.9)=71.2 N`