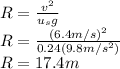Question

What is the smallest radius of an unbanked (flat) track around which a bicyclist can travel if her speed is 23 km/h and the coefficient of static friction between tires and track is 0.24?

Answer 1

Step-by-step explanation:

Below is an attachment containing the solution.

Answer 2

`R=17.4m`

Step-by-step explanation:

Given data

Speed v=23 km/h =6.4 m/s

Coefficient of static friction μs=0.24

The acceleration experienced by bicycle is centripetal acceleration by:

`\alpha =(v^2)/(R)`

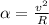
This acceleration is only due to static friction force given by:

`f=m(v^2)/(R)`

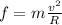
The maximum value of the static friction force given by

`f_(s.max)=u_(s)F_(N)\\Where\\F_(N)=mg`

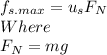
Therefore when the car is on verge of sliding:

`f=f_(s.max)\\m(v^2)/(R)=u_(s)mg`

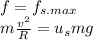
Therefore the minimum radius the bicycle can move without sliding is:

`R=(v^2)/(u_(s)g)\\ R=((6.4m/s)^2)/(0.24(9.8m/s^2)) \\R=17.4m`