Question

A ball is thrown into the air and its position is given by h ( t ) = − 6.3 t 2 + 53 t + 24 where h is the height of the ball in meters t seconds after it has been thrown. Find the maximum height reached by the ball and the time at which that happens.

Answer 1

`h'(t) = -12.6 t +53`

Now we can set up the derivate equal to 0 and we have:

`-12.6 t +53 = 0`

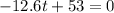
And solving for t we got:

`t = (53)/(12.6)= 4.206`

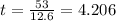
For the second derivate respect the time we got:

`h''(t) = -12.6<0`

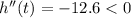
So then we can conclude that t = 4.206 is a maximum for the function.

And the corresponding height would be:

`h(t=4.206) = -6.3(4.206)^2 +53*4.206+24= 135.468 ft`

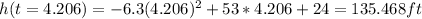
So the maximum occurs at t = 4.206 s and with a height of 135.468 m

Explanation:

For this case we have the following function:

`h(t) = -6.3t^2 +53 t+24`

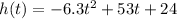
In order to maximize this function we need to take the first derivate respect the time and we have:

`h'(t) = -12.6 t +53`

Now we can set up the derivate equal to 0 and we have:

`-12.6 t +53 = 0`

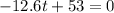
And solving for t we got:

`t = (53)/(12.6)= 4.206`

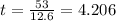
For the second derivate respect the time we got:

`h''(t) = -12.6<0`

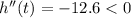
So then we can conclude that t = 4.206 is a maximum for the function.

And the corresponding height would be:

`h(t=4.206) = -6.3(4.206)^2 +53*4.206+24= 135.468 ft`

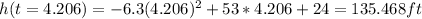
So the maximum occurs at t = 4.206 s and with a height of 135.468 m