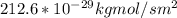Answer:
a. Therefore, the flux in kg mol/s.m² at N₂ =
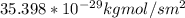
b. Therefore; when temperature = 473k , the flux (J) decreases.
c. Hence, when T = 298K, but the total pressure = 3.0 atm , the flux increases.
d. The CO flux for part C =
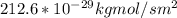
Step-by-step explanation:
Given that :
Equimolar counter-diffusion
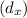 = 0.11 m
= 0.11 m
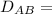
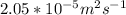
T = 298 K
For ideal gas equation:
PV = nRT
Making V the subject of the formula:
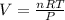
where the number of moles (n) =
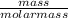
∴ the V =
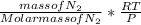
V =
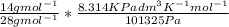
V =
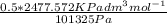
V =
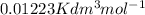
V =
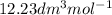
V =
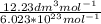
V =
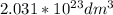
V =
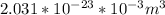
V =
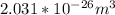
The volume of N₂ =
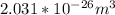
Density of
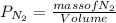
=
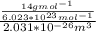
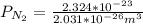
=
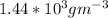
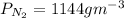
Now, The flux (J) =
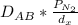
J =
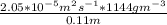
J =
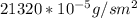
J =
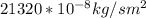
J =
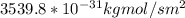
J =
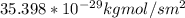
Therefore, the flux in kg mol/s.m² at N₂ =
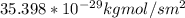
b. At T = 473 K
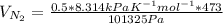
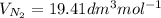
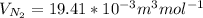
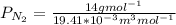
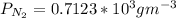
J =
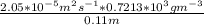
J =
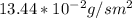
J =
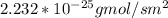
J =
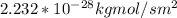
J =
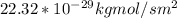
Therefore; when temperature = 473k , the flux (J) decreases.
c. At P = 3 atm = 3×101325 Pa
T = 298 K
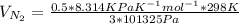
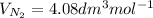
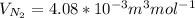
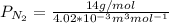
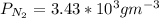
J =
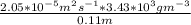
J =
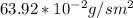
J =
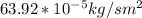
To moles; we have:
J =
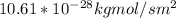
J =
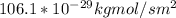
Hence, when T = 298K, but the total pressure = 3.0 atm , the flux increases.
d. We can determine the CO flux for part c as follows:
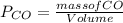
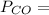
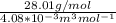
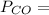
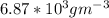
J =
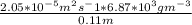
J =
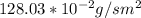
J =
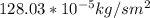
J =
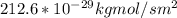
The CO flux for part C =