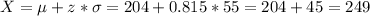Question

New York City is the most expensive city in the United States for lodging. The room rate is $204 per night (USA Today, April 30, 2012). Assume that room ratesa mally distributed with a standard deviation of $55. a. What is the probability that a hotel room costs $225 or more per ni b. What is the probability that a hotel room costs less than $140 per n c. What is the probability that a hotel room costs between $200 and $300 per ni me 25. are nor ght? ight? d. What is the cost of the most expensive 20% of hotel rooms in New York City?

Answer 1

a. P=0.35

b. P=0.12

c. P=0.49

d. Cost: more than $249 per night.

Explanation:

We assume a normal distribution with mean $204 and s.d of $55.

To calculate the probability we calculate the z-value for each case

a. What is the probability that a hotel room costs $225 or more

`z=(X-\mu)/(\sigma)=(225-204)/(55)= (21)/(55)= 0.382\\\\P(X>225)=P(z>0.382)=0.35`

b. What is the probability that a hotel room costs less than $140

`z=(140-204)/(55)= (-64)/(55)=-1.164\\\\P(X<140)=P(z<-1.164)=0.12`

c. What is the probability that a hotel room costs between $200 and $300

`z=(200-204)/(55)= (-4)/(55)=-0.073\\\\P(X<200)=P(z<-0.073)=0.47\\\\\\z=(300-204)/(55)= (96)/(55)=1.745\\\\P(X<300)=P(z<1.75)=0.96\\\\\\P(200<X<300)=P(X<300)-P(X<200)=0.96-0.47=0.49`

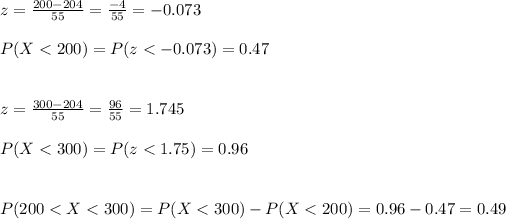
d. What is the cost of the most expensive 20% of hotel rooms in New York City?

In this case, we have to estimate z' so thats P(z>z')=0.2. This value is z=0.841.

Then, the value of X should be:

`X=\mu+z*\sigma=204+0.815*55=204+45=249`