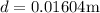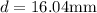The smallest allowable depth is
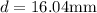 for the milled portion of bar.
for the milled portion of bar.
Step-by-step explanation:
Given,
Magnitude of force,
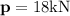
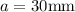
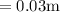
Allowable stress,
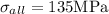
cross sectional area of bar,
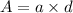
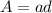
e - eccentricity
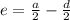
The internal forces in the cross section are equivalent to a centric force P and a bending couple M.
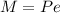
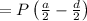
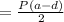
Allowable stress
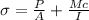
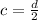
Moment of Inertia,
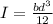
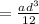
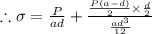
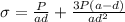
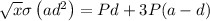
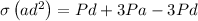
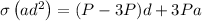
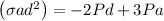
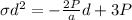
By substituting values we get,
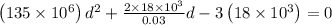
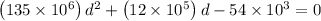
On solving above equation we get,